《星际战甲(Warframe)台服》【问题】尝试了解官方公布的紫卡交易数据

但假如你对这些数字并不了解，或者不知道市场上的走向。

这篇文可能帮得上你。

如果你非常熟悉使用网上各种查价工具

或者你已经学过统计学，明白这些数字背后的意义是甚幺

也欢迎你逗留一下，帮我看看有没有错误。

目前网上已经有一定量的紫卡查价工具，

只要输入你的紫卡武器、属性、数值，你可以得出一个大约的价格。

但在这篇文并不是介绍各种查价工具或另一串紫卡问价片，

不，绝对不是。

这篇文是尝试解释官方给出的交易数据，来猜测紫卡市场上的情况。

但是现时官方给出的数据并没有办法完全推算出真实的状况。

只能大概去知道发生甚幺事。

下面我会提及一些统计学或数学的用词，你或者听过，或者没有。

但是这没关係，因为我解释一下。

---

PC︰http://n9e5v4d8.ssl.hwcdn.net/repos/weeklyRivensPC.json

PS4︰http://n9e5v4d8.ssl.hwcdn.net/repos/weeklyRivensPS4.json

XB1︰http://n9e5v4d8.ssl.hwcdn.net/repos/weeklyRivensXB1.json

Switch︰http://n9e5v4d8.ssl.hwcdn.net/repos/weeklyRivensSWI.json

先给一下资料来源，上面是交易资料。

在里面你会见到像这样的几行

"itemType" : "Kitgun Riven Mod",

这是指甚幺类型的武器，步枪、霰弹、手枪、近战、kitgun、zaw

"compatibility" : null,

这是指这紫卡是那个武器的，例如︰捕月，Null是指未开启。

"rerolled" : false,

这是指紫卡有没有被重骰，如果有就True，没有就Flase

"avg" : 30.08,

这是同一个武器的各张紫卡，交易金额的平均数。

"stddev" : 32.85,

这是同一个武器的各张紫卡，交易金额的标準差。

"min" : 3,

这是同一个武器的各张紫卡，交易金额的最低一个数值(最便宜)

"max" : 1000,

这是同一个武器的各张紫卡，交易金额的最高一个数值(最昂贵)

"pop" : 2.5712,

这是这武器的紫卡交易热门度，未知计算方式

"median" : 30
这是同一个武器的各张紫卡，最中间的那一个交易金额。

计算的方式各有不同，而呈现出的效果也有所不同，因此给予的数据分析方法越多，能知道更详细。

由Min 及 Max，我们只能知道所有紫卡的售价都在这个範围裏面︰

Min 3<---------->1000 Max

但是我们并不能知道他们的分布是怎样的，即是说，他们可以在以下的方式排列︰

Min 3 < o-o-oo-o-oo-o-o > 1000 Max 或者

Min 3 < ooo-oo----o-ooo > 1000 Max

我们很明显看出，这两个是不同的，但是它们仍然是在3-1000这个範围裏。

然后，我们用一个更有效的方法，用计算平均数的方法，来尝试得出一个指标︰

这样的话，我们应该可以找得到一个大约中间的指标，最首最尾加起来除，应会得出两者中间的答案，所以，应该是可以有些指标性的。

由刚刚的例子可以看到一些︰

Min 3, Max 1000, avg, 30

3 <---------------------------------> 1000

儘管最小的交易金额是3，最高是1000，平均数却是30，而不是500。

这样我们可以得到几个可能︰

低于，或者等于30白金的紫卡交易数是主流

高于30的是少数，或者非常少数。

再加一个指标︰中位数

中位数是一个所有数字由大小排序后，取最中间的一个。

假如这类紫卡以9个不同价格售出︰3,10,12, 18, 30, 30, 32, 35, 1000

最中间的就是第5个，即是 [30]。

平均数、中位数都是大约[30白金]时，我们都可以说，30真的是中间的数字

但是如果这样呢...下面两个的平址数跟中位都是一样的时候，我们有甚幺办法?

< oooo-----o-----oooo >

< oo---oo--o--oo---oo >

这时候就要加入「标準差」这个方法

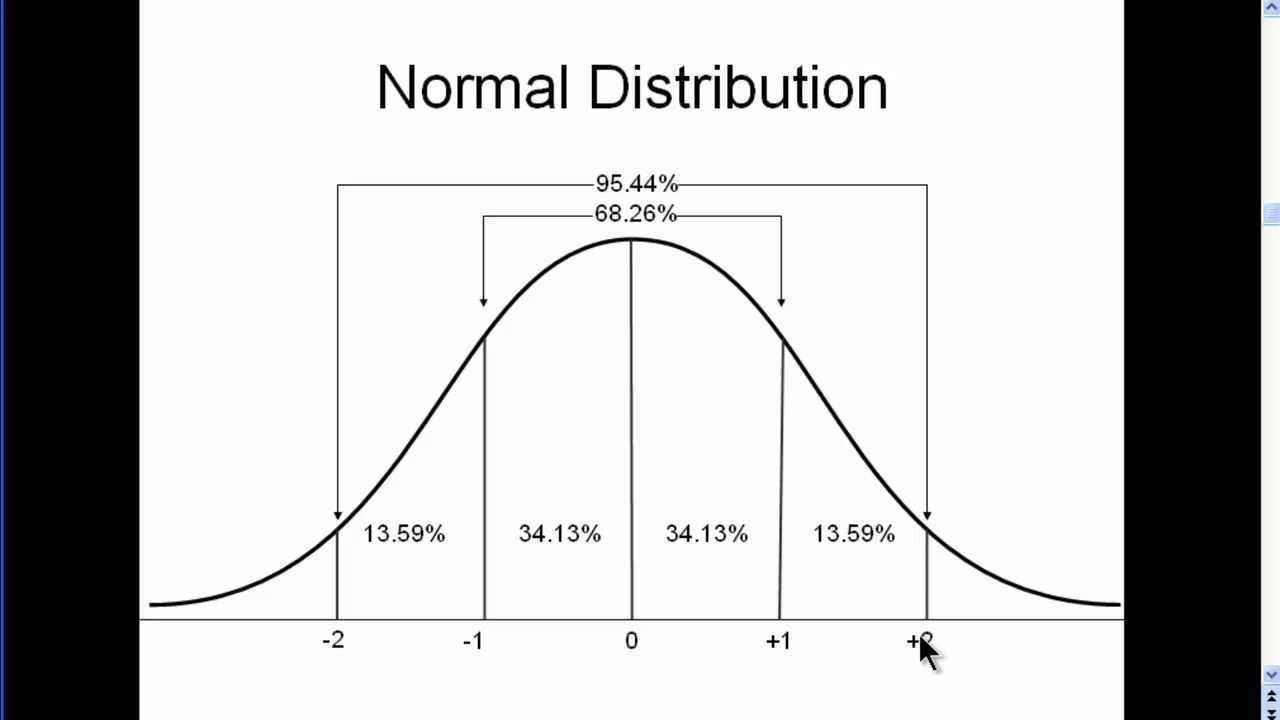
「标準差」有一个挺有趣的特性，我们本来假设一个正常的数据，是会这样的︰

这个叫Normal distribution curve，一般来说︰

最高及最低是少数

靠中间的会很多

然后看看刚刚的数据，kitgun的std是︰32.85

如何去读呢…

1. 找出平均数，然后标示为0，30->0

2. 把这个数字加或减 (std*1)，然后标为1/-1，-2.85(0) ->(-1)，62.85(1)

3. 把这个数字加或减 (std*2)，然后标为2/-2，-35.7(0) ->(-2)，95.7(2)

4. 把这个数字加或减 (std*3)，然后标为3/-3，-68.55(0) ->(-2)，128.55(2)

计算完标準差后，我们得出一个很有趣的结论︰

由-1至1，是覆盖了68.26%的数据，即是说 68.26%的kitgun紫卡交易金额，是由0至62.85白金

由-2至2，是覆盖了95.44%的数据，即是说 95.44%的kitgun紫卡交易金额，是由0至95.7 白金不等

剩下的交易，只佔了所有交易的4.5%左右。

虽然这些数字是可以有这种解释，但是像刚刚例子的数字

除了知道大部分紫卡是徘徊在0-95外，其实很难知道其他的资讯。

不过每月去看这些资料时，就会出现另一个有趣的资讯，就是趋势了。

但是正态(常态)分布并不是这幺容易出现的，它很完美，是理想中的形状。

但是现实都是不完美的，所以分布跟形状都有不同。

偏度跟峰度(或过剩峰度)就能用来描述这个形状，给予一个大概的数据。

偏度是指数据较为偏向、集中在整个数据列的哪一个部分。

偏度等于0时，就是正态分布

少于0时，数据集中在较大的数字的方向，右边较高，尾巴指向负数。

大于0时，数据集中在较小的数字的方向，左边较高，尾巴指向正数。

偏度计算方式︰有很多种，我只懂得一种 (Pearson skewness coefficient #2)